|
|
If $$\frac{7x} 3+a=8$$ and $$a > 8$$, then, in terms of a, $$\frac{3x} 7=$$
|
|
|
If $$x > 0$$, then $$\frac1 {\sqrt{2x}+\sqrt{x}}$$ =
|
|
|
In the sequence of nonzero numbers $${t}_{1}$$, $${t}_{2}$$, $${t}_{3}$$, ..., $${t}_{n}$$, ..., $${t}_{n+1}=\frac{{t}_{n}}{2}$$ for all positive integers n. What is the value of $${t}_{5}$$?(1) $${t}_{3}=\frac{1}{4}$$(2) $${t}_{1}-{t}_{5}=\frac{15}{16}$$
|
|
OG18-数学分册
|
The product of 3,305 and the 1-digit integer x is a 5-digit integer. The units (ones) digit of the product is 5 and the hundreds digit is y. If A is the set of all possible values of x and B is the set of all possible values of y, then which of the following gives the members of A and B ?
|
|
Magoosh
|
If 4x - 3y = 13 and 5x + 2y = -1, then x =
|
|
Magoosh
|
If x + |x| + y = 7 and x + |y| - y = 6 , then x + y =
|
|
Manhattan
|
In the rectangular coordinate plane points X and Z lie on the same line through the origin and points W and Y lie on the same line through the origin. If$$ a^{2} + b^{2} = c^{2} + d^{2} and e^{2} + f^{2} = g^{2} + h^{2}$$, what is the value of length XZ – length WY?
|
|
OG18-数学分册 OG19-数学分册
|
If a, b, and c are constants, a > b > c, and $$x^{3} ‒ x = (x ‒ a)(x ‒ b)(x ‒ c)$$ for all numbers x, what is the value of b ?
|
|
OG19 OG20 OG2022
|
In the xy-coordinate plane, if the point(0, 2)lies on the graph of the line 2x+ky =4, what is the value of the constant k?
|
|
OG19-数学分册
|
$$\frac{2\frac{3}{5}-1\frac{2}{3}}{\frac{2}{3}-\frac{3}{5}}$$=
|
|
Ready4
|
If a, b, and c are constants and  and  , for all numbers  , what is the value of  ?
|
|
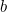PREP07 Test 2
|
If $$(\frac{2}{3})^{n}=(\frac{3}{2})^{2}$$, what is the value of n ?
|
|
PREP07 Test 1
|
If -3 is 6 more than x, what is the value of $$\frac{x}{3}$$
|
|
OG21 OG2022
|
If the units digit of $$\frac{5610.37}{10^{k}}$$ is 6, what is the value of k?
|
|
Magoosh
|
If$$(\frac{1}{2})^{24}(\frac{1}{81})^{k}={{1}\over18^{24}}$$ , then k =
|
|
190310
|
$$B_n=A_{n+1}-A_{n},B_{n+1}-B_{n}=2$$.$$A_{10}$$=?
1: $$A_1=1,A_3=3$$
2: $$A_2=2,A_4=4$$
|
|
OG12 OG15 OG16 OG17
|
Is the number of seconds required to travel $${d}_{1}$$ feet at $${r}_{1}$$ feet per second greater than the number of seconds required to travel $${d}_{2}$$ feet at $${r}_{2}$$ feet per second?(1)$${d}_{1}$$ is 30 greater than $${d}_{2}$$.(2)$${r}_{1}$$ is 30 greater than $${r}_{2}$$.
|
|
181215
|
If $$\frac{1}{n(n+1)}$$ - $$\frac{1}{(n+1)(n+2)}$$ = $$\frac{2}{n(n+1)(n+2)}$$ , so $$\frac{2*9900}{3*4*5}$$+$$\frac{2*9900}{4*5*6}$$+......+$$\frac{2*9900}{98*99*100}$$=?
|
|
200301 还原机经选题: 数论&代数
|
If n, m, and k are positive integers, and $$\frac { 9 } { 10 } < \frac { 1 } { n } + \frac { 1 } { m } + \frac { 1 } { k } < 1$$, is n+m+k >11?
(1)n=2 and m=3
(2)k=7
|
|
|
In the formula $$V =\frac{1}{(2r)^3}$$,if r is halved, then V is multiplied by
|