|
Magoosh
|
K is a set of integers such thati) if x is in K, then 2x is in Kii) if each of x and y is in K, then x + y is in KIs 15 in K?(1) 1 is in K.(2) 3 is in K.
|
|
OG18-数学分册
|
K is a set of numbers such that (i) if x is in K, then -x is in K,and (ii) if each of x and y is in K, then xy is in K.Is 12 in K?(1) 2 is in K.(2) 3 is in K.
|
|
OG19-数学分册
|
K is a set of numbers such that
(i) if x is in K, then -x is in K, and
(ii) if each of x and y is in K, then xy is in K.
Is 12 in K?
(1) 2 is in K.
(2) 3 is in K.
|
|
几何
|
If k is an integer and 2 < k < 7, for how many different values of k is there a triangle with sides of lengths 2,7, and k ?
|
|
Magoosh
|
Set K consists of 4 integers. What is the median of K?(1) The average (arithmetic mean) of K is 3.(2) The mode of K is 3.
|
|
Magoosh
|
If$$\sqrt{k}$$ is not an integer, then is K a prime number?Statement #1: K < 10Statement #2: K < 5
|
|
Magoosh
|
If k is the greatest positive integer such that$$ 3^{k}$$ is a divisor of 15! then k =
|
|
190321
|
(k-1)x=5.Is x>1.25?'
1:k is a positive integer.
2:k>5
|
|
|
If k is a positive integer, what is the remainder when $${2}^{k}$$ is divided by 10 ?(1) k is divisible by 10.(2) k is divisible by 4.
|
|
|
If n and k are positive integers, is n divisible by 6?(1)n = k(k + 1)(k - 1)(2)k - 1 is a multiple of 3.
|
|
Magoosh
|
What is the value of k?(1)$$ k^4 = \frac{1}{625}$$(2)$${ k^3} < k^2$$
|
|
OG15 OG16 OG17 OG18 OG19 OG20 OG2022
|
If k is an integer such that 56 < k < 66, what is the value of k ?(1) If k were divided by 2, the remainder would be 1(2) If k + 1 were divided by 3, the remainder would be 0.
|
|
PREP07 Test 2
|
If k and t are integers and $$k^2 - t^2$$ is an odd integer, which of the following must be
an even integer?I. k+t+2II. $$k^2+2kt+t^2$$III. $$k^2+t^2$$
|
|
PREP07 Test 1
|
If the product of the three digits of the positive integer k is 14, what is the value of k?(1)k is an odd integer.(2)k < 700
|
|
300难题
|
 Let n and k be positive integers with $$ k\leq n$$. From an n * n array of dots, a k * k array of dots is selected. The figure above shows two examples where the selected k * k array is enclosed in a square. How many pairs (n,k) are possible so that exactly 48 of the dots in the n * n array are NOT in the selected k * k array?
Let n and k be positive integers with $$ k\leq n$$. From an n * n array of dots, a k * k array of dots is selected. The figure above shows two examples where the selected k * k array is enclosed in a square. How many pairs (n,k) are possible so that exactly 48 of the dots in the n * n array are NOT in the selected k * k array?
|
|
Magoosh
|
If k is an integer and $$121 < k^{2} < 225$$, then k can have at most how many values?
|
|
Ready4
|
If  and and 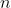 are integers, is are integers, is ) odd? odd?
(1)  is odd. is odd.
(2) 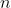 is odd. is odd.
|
|
191031 还原机经选题: 数论&代数
|
If k and n are positive factors, and f(n) represents the remainder when n is divided by k,is k>10?
(1)f(k+32)=8
(2)f(k+42)=6
|
|
OG18-数学分册
|
If x and k are integers and $$({12}^{x})({4}^{2x+1})=({2}^{k})({3}^{2})$$, what is the value of k?
|
|
|
What is the value of the integer k?(1)$$k + 3 > 0$$(2)$${k}^{4}\le{0}$$
|