|
Magoosh
|
In a certain sock drawer, there are 4 pairs of black socks, 3 pairs of gray socks and 2 pairs of orange socks. If socks are removed at random without replacement, what is the minimum number of socks that must be removed in order to ensure that two socks of the same color have been removed?
|
|
Magoosh
|
If f(x) = $$12-{x^{2}\over{2}}$$and f(2k) = 2k, what is one possible value for k?
|
|
Magoosh
|
If$${(\frac{1}{x}+x)}^{2}=16$$,then $${{1}\over{x^{2}}}+x^{2}=$$
|
|
Magoosh
|
How many points (x, y) lie on the line segment between (22, $$12\frac {2}{3})$$ and (7,$$ 17 \frac{2}{3}$$) such that x and y are both integers?
|
|
Magoosh
|
If x is a number such that $$x^2 + 2x - 24 = 0 and x^{2} + 5x - 6 = 0$$, then x =
|
|
Magoosh
|
If$$\sqrt{17+\sqrt{264}} $$ can be written in the form $$\sqrt{a}+\sqrt{b}$$ , where a and b are integers and b < a, then a - b =
|
|
Magoosh
|
If k is an integer and $$121 < k^{2} < 225$$, then k can have at most how many values?
|
|
Manhattan
|
If a and b are positive integers and$$ x = 4^{ a} and y = 9^{ b}$$, which of the following is a possible units digit of xy?
|
|
OG18-数学分册
|
If r and s are positive integers such that$$ ({2}^{r})(4^{s}) = 16$$, then $$2r + s =$$
|
|
OG18-数学分册
|
The number 2 ‒ 0.5 is how many times the number 1 ‒ 0.5 ?
|
|
OG18-数学分册
|
Points A, B, C, and D, in that order, lie on a line. If AB = 3 cm, AC = 4 cm, and BD = 6 cm, what is CD, in centimeters?
|
|
OG18-数学分册
|
A certain bridge is 4,024 feet long. Approximately how many minutes does it take to cross this bridge at a constant speed of 20 miles per hour? (1 mile = 5,280 feet)
|
|
OG18 OG19 OG20 OG2022
|
If k is a positive integer, what is the remainder when $$(k + 2)({k}^{3} – k)$$ is divided by 6 ?
|
|
Ready4
|
If 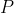 and and 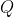 are sets of integers, are sets of integers,  denotes the set of integers that belong to set denotes the set of integers that belong to set 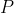 or set or set 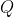 , but not both. If , but not both. If 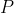 consists of 15 integers, consists of 15 integers, 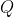 consists of 8 integers, and 4 integers are in both consists of 8 integers, and 4 integers are in both 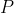 and and 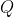 , then , then  consists of how many integers? consists of how many integers?
|
|
模考带练机经题
|
How many different prime factors does 2730 have?
|
|
模考带练机经题
|
If 12! is a multiple of $$(4!)^{n}$$ and not a multiple of $$(4!)^{n+1}$$, what is the value of n?
|
|
190124
|
There is a stack of cards. 9 cards are blue and the rest are red. The probability of taking out two cards randomly that are both blue is 1/7. What's the number of the red cards?
|
|
190124
|
4 < $$x^{2}$$ -2x +1 < 16,How many integers x satisfy the inequality?
|
|
181215
|
How many solutions does the equation $$\frac{x^{2}-1}{x-1}$$=0 have?
|
|
181215
|
Coffee cups were put in two size of boxes. A big box and a small box can hold 15 coffee cups. Two big boxes and four small boxes can hold 40 coffee cups. How many coffee cups can be put in a big box?
|